Why don't we use Ternary Search?

Before answering the question in the title, let’s see a bit about Binary Search.

Binary Search is one of the most basic algorithms that every programmer learns. The gist of it is simple. To search for an element in a sorted array, compare the search key with the middle element.

• If both are the same, we have found the element.
• Else if the key is lesser than the middle element, Repeat the search in the left subarray.
• Else repeat the search in the right subarray.
• if there is no such subarray to search then the element does not exist in this array.

Why is Binary search efficient?

The algorithm is simple and with each comparison, we are cutting the search space in half.

This quickly adds up; to search an array with a million elements, we will need at most just 20 such comparisons. Compare this to the million comparisons we would need if we took the naive approach of checking each element till we find the one we are searching for.

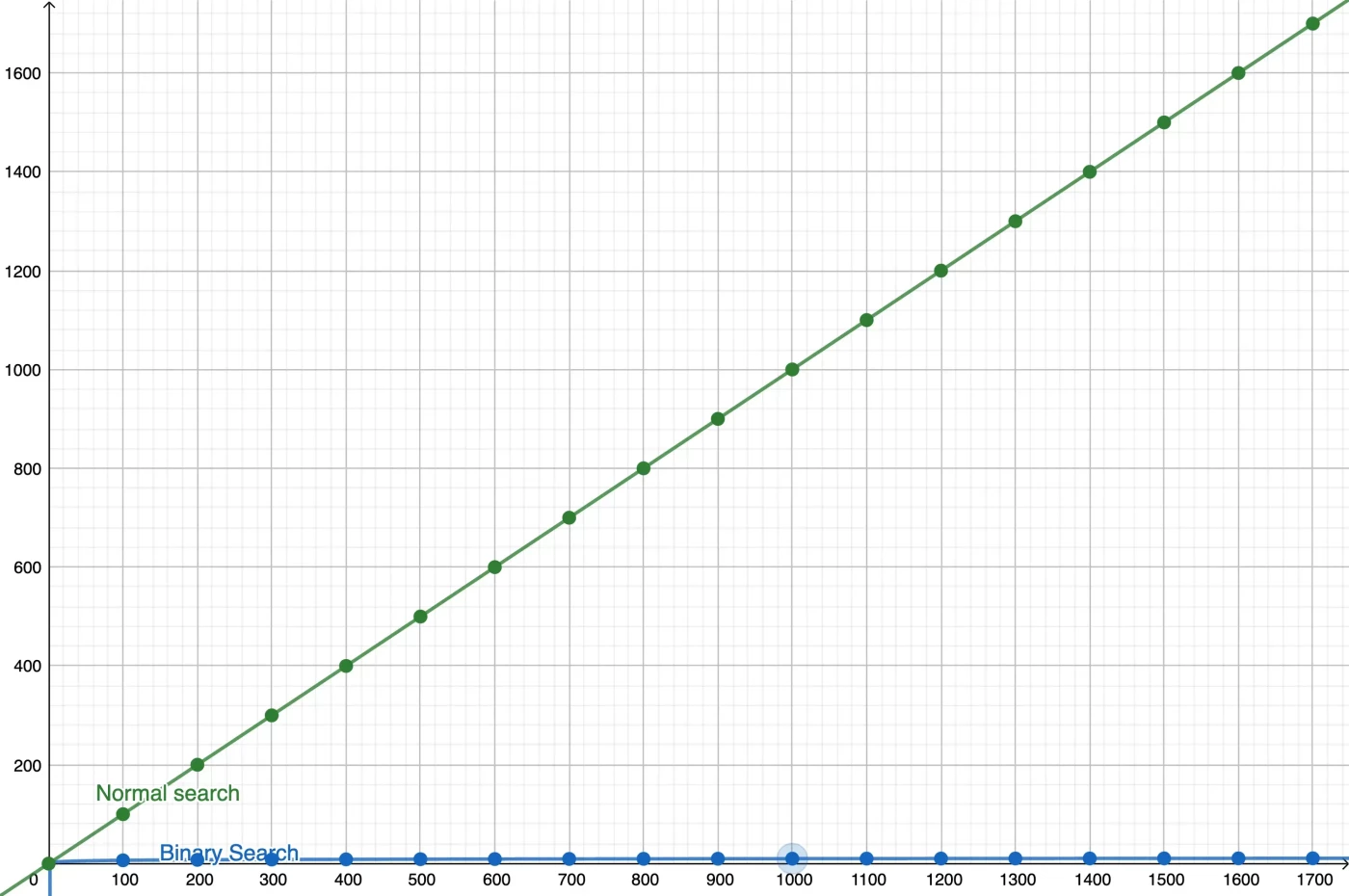
Ternary Search should be better, right?

At each level, Instead of cutting the search space in half (50%) what if we narrowed it down to just (33%) by splitting the array into 3 parts instead of 2?

It seems like ternary search should be more efficient than binary search, after all, O(log₃ (n)) should be faster than O (log₂ (n)) right?

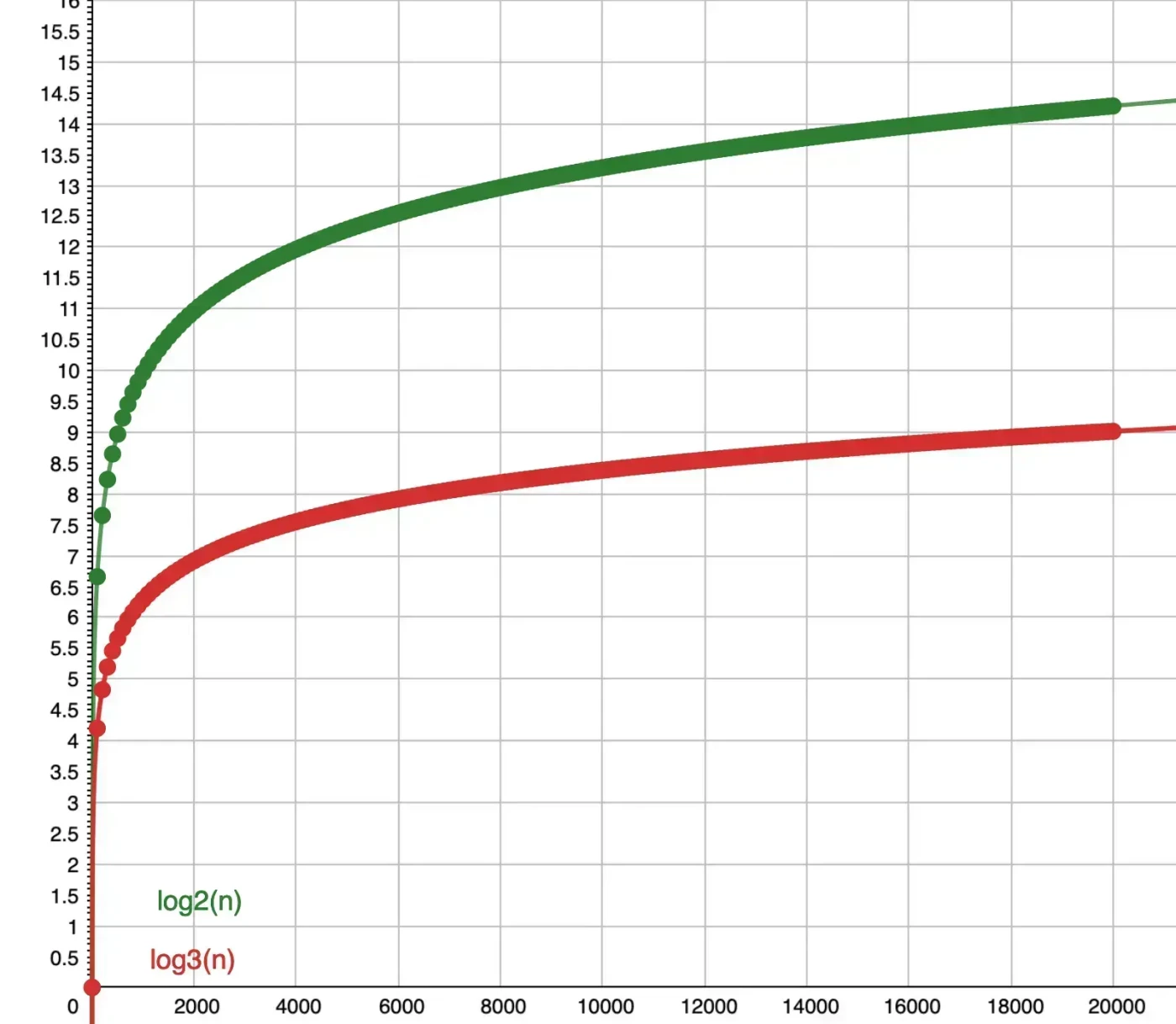
But there is a catch, in Binary search we need only one comparison at each level - we just compare the search key with the middle element - but in Ternary search, we need 2 comparisons: compare with the element at index n/3 and then with the element at index 2*n/3.

So in reality the time complexity of Ternary Search is not log₃(n) but 2 * log₃(n).

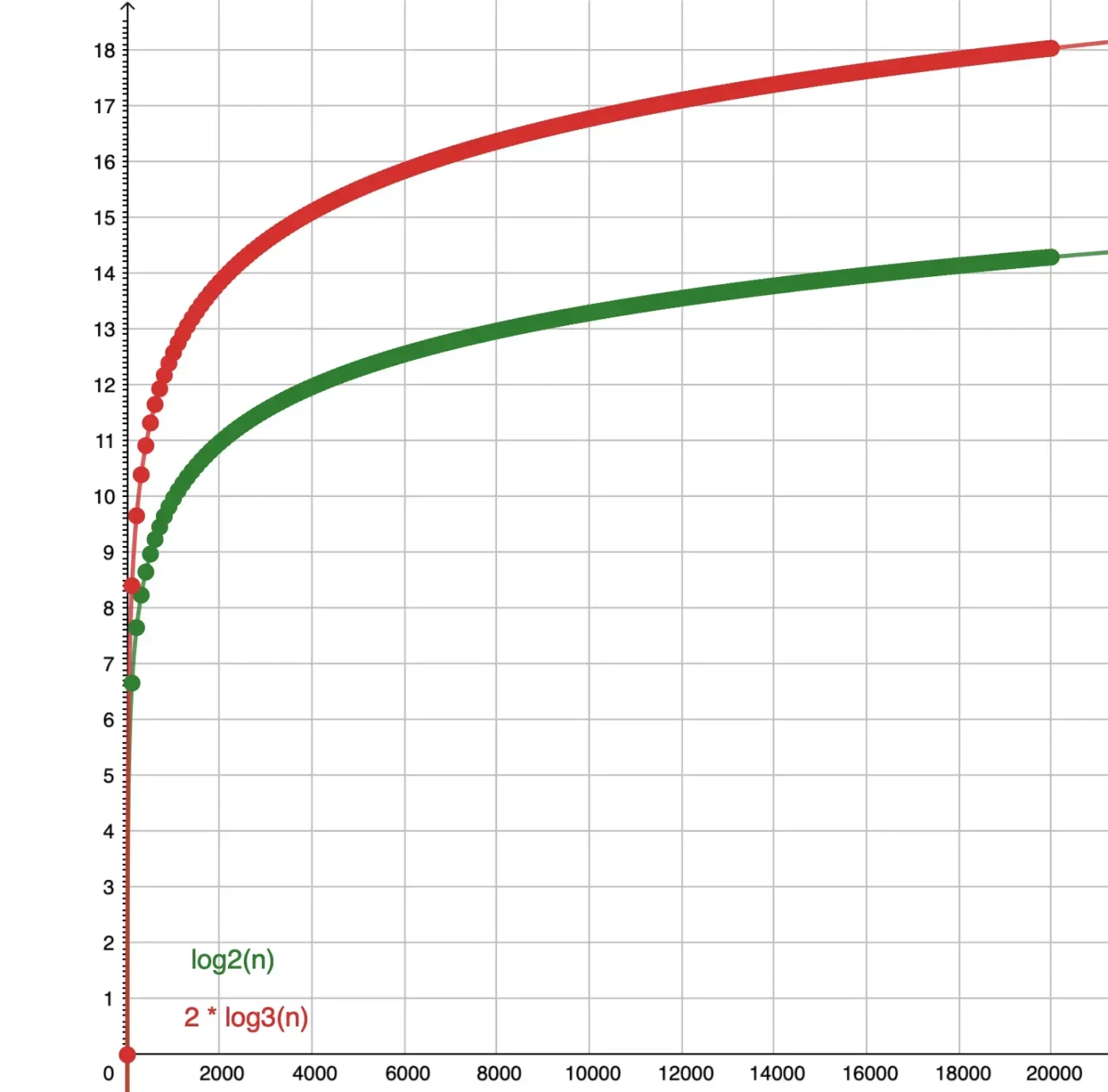
Even though 2 * log₃(n) is still O(log₃(n)) as per Big-Oh notation, the constants have a real-world impact in this case.

Split	No. of Comparisons at each level	Max Comparisons for searching in n elements (n = 1000)	n = 10000	n = 100000
2	1	10	14	17
3	2	13	17	21
4	3	15	20	25
5	4	18	23	29
6	5	20	26	33
7	6	22	29	36

As we can see from the table, Binary Search (Split 2) is better than Ternary Search (Split 3) or any other n-ary splits for searching a single element.

Why is binary search special?

Because we and our computers are special and can compare only 2 elements at a time, if we could somehow compare three elements in a single operation, then ternary would be optimal.

Ternary Search is not without its uses, a variation of the three-split search can be used for finding the max or min element in an array if the array has a single highest or lowest element.